カーリング・ストーンが氷を削るメカニズム

ストーンが滑ると氷くずが生じるのはなぜ？

ストーンに作用する抵抗は、ランニング・バンドと氷の間の摩擦と考えられています。しかし、一つ疑問が生まれます。それは、ランニング・バンドと氷の平面同士の摩擦ならば氷は削られない筈ですが、実際には、ストーンが滑ると必ず「氷くず（アイス・デブリ）」が生じるからです。ランニング・バンドの表面はピカピカではありませんが滑らかな平面に仕上げられており、とても氷を削るとは考えられません。しかし、カーラーたちは、投げる前には必ずストーンの底の窪みに溜まった氷くずを取り除きますし、どの競技場でも、競技や練習が終わると氷上に生じた白い氷くずを清掃する必要があります。氷くずを生じる摩擦以外のメカニズムとは、一体何でしょうか？

この問題に対するヒントを私は2018年に思いつき、それを基礎にしてストーン運動の新しい理論「エッジ切削モデル」を組み立てました^(1)(2)(3)(4)。ヒントはランニング・バンドの独特の形状に関係しています。上で書きましたように、ランニング・バンドは一定の幅をもったドーナツ状の平面です。当然のことですが、バンドの両側は文字通り「端（エッジ、edge）」です。そして、同時にそれは角度や鋭さによっては「刃（エッジ、edge）」の働きをすることに気が付いたのです。

図１の模式図から明らかなように、ストーンが矢印の方向に進むとき、ぺブルに出会うのはピンクで描いた前面ランニング・バンドの外側エッジです。グレーで描いた後面ランニング・バンドは内側エッジでぺブルに出会います。エッジとぺブルの出会いは、背の低いぺブルなら滑らかで何事も起きませんが、背の高いぺブルならミクロな衝突となり、氷の変形、破壊、切削が起こります。もちろん、どのカーリング場でもぺブルは出来る限り一定の高さになるように整備しています。しかし、どうしても0.1ミリほどの高低は生じてしまいます。その結果、ストーンが滑るとエッジはぺブルを削り、氷くずを生成すると考えられます。

ストーンに働くエッジ切削抵抗

カーリングの世界では「ランニング・バンド」「ランニング・サーフェイス」「ランニング・エッジ」等の呼び名がほぼ同じ意味で使われています。しかし、エッジには「刃」の意味もあり、ランニング・エッジは単なる平面ではなく氷を削ることを連想させます。この後述べますように、エッジがぺブルを削る時の力は「エッジ切削抵抗」としてストーンの運動に重要な影響を与えます。

図２にエッジがぺブルに出会う時の様子を模式的に描きました。上が側面図で下が平面図です。エッジ角θはエッジの鋭さを示します。ストーンの速度はV、角速度はω、エッジとストーン中心の距離はrです。従って、エッジは、W=rωの回転速度で横方向に移動しながら、並進速度Vでぺブルを切削し、その過程でエッジ切削抵抗Gの力を発生していることになります。前面ランニング・バンドの外側エッジおよび後面ランニング・バンドの内側エッジは、出会うすべてのぺブルからエッジ切削抵抗を受け、その総和がストーンの重心に働き、ストーンの運動に重要な影響を与えます。

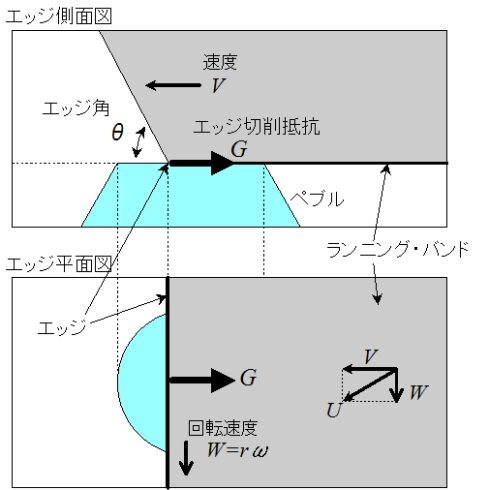
図2 エッジとぺブルの模式図

エッジ切削抵抗(G)は、エッジ角(θ)、ストーンの並進移動速度(V)、回転速度(W)の関数。
rとωはそれぞれランニング・バンドの半径と回転角速度。

エッジ切削抵抗の式

上の話をまとめると、エッジ切削抵抗は少なくとも３個の因子(θ,V,W)の関数ということになります。ストーン運動のエッジ切削モデルでは、この関数形を明らかにし数値計算を進めました。エッジ切削抵抗とエッジ角との関係(G–θ)は、Lieu-Moteの氷で行った実験結果⁽⁵⁾から求めることができます(図３)。エッジ切削抵抗には、エッジ角の増加とともに増えるべき乗の関数(θ^1.41)が得られました。

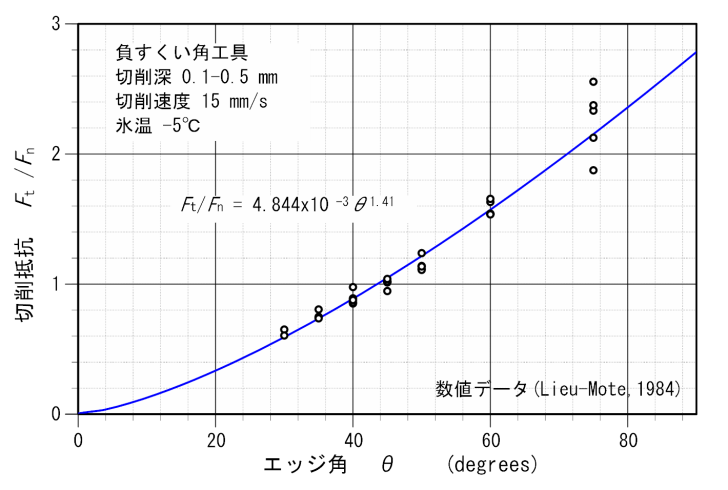
図3 切削抵抗とエッジ角の関係

切削抵抗はエッジ角の増加とともに増える。切削抵抗は垂直応力との比で示してある。
数値データはLieu-Mote(1984)の図8と図9から読み取った⁽⁵⁾。

G–VとG–Wの関係に関してはこれまで氷を使っての計測は行われたことがありません。そのため、他物質の結果を参考にすることにしました。図４は珪石他の鉱物を使って行われた多数の計測データ⁽⁶⁾から求めたG–Vの関係です。エッジ切削抵抗は切削速度の増加とともにべき乗(V^-0.319)の形で減少します。この関数の形は氷の場合にも適用できると仮定して使用することにします。

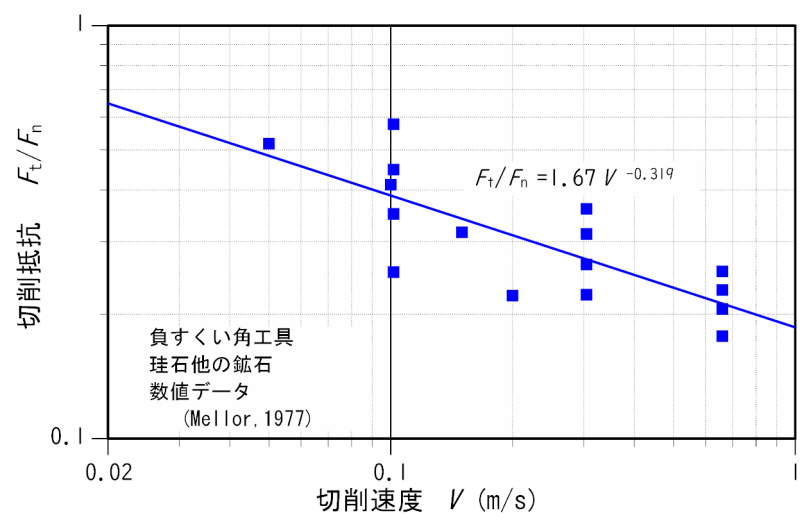
図4 切削抵抗と並進速度の関係

切削抵抗はストーンの並進速度の増加とともに減少する。切削抵抗は垂直応力との比で示してある。
数値データはMellor(1977)の図56、図57、図58から読み取った⁽⁶⁾。

最後にG–Wの関係ですが、このような特殊な条件の計測は、氷だけでなく他の物質に関しても行われたことがないようです。これまで述べませんでしたが、切削工学や研削工学あるいはトライボロジーの分野では、包丁のような工具は「正のすくい角工具」と呼び、やすり、研磨粒子、摩耗粒子等による研磨や摩耗のような場合は「負のすくい角工具」と呼んで区別しています。この定義に従いますと、ランニング・バンドのエッジは負のすくい角工具ということになりますが、このような場合の切削抵抗をエッジの２方向の速度の関数として計測したデータは到底手に入りそうにありません。そのため、正のすくい角工具である通常の包丁による計測結果を使うことにしました。

その結果が図５です。これは、和食において刺身を綺麗にかつ美味しい味に切る、いわゆる「引き切り」の場合の計測データ⁽⁷⁾です。包丁の垂直方向の切削速度を一定に保ち、水平方向の速度、つまり引く速さをいろいろかえて切削抵抗を測定した結果です。切削抵抗は水平速度が増加すると指数関数EXP(-3.42W)の形で減少しています。Wは水平切削速度です。はやく引くほど包丁に加える力は小さくてよく、そのため魚肉に無駄な負担がかからないようです。この結果をカーリング・ストーンに当てはめると、ストーンの回転速度が増えるほどエッジ切削抵抗は小さいことを意味します。

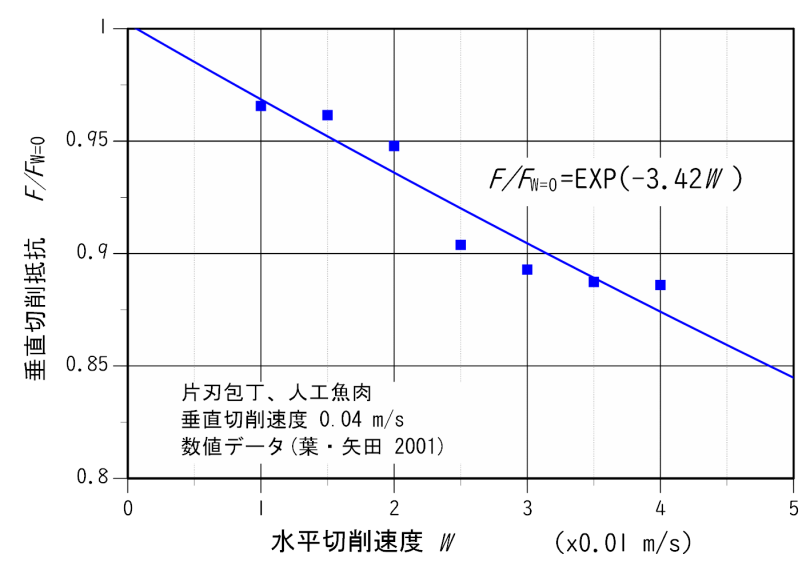
図5 切削抵抗と回転速度の関係

切削抵抗はストーンの回転速度の増加とともに減少する。切削抵抗は水平速度がゼロの時の値との比で示してある。数値データは葉・矢田(2001)の図6から読み取った⁽⁷⁾。

以上の結果を一つの式にまとめると、エッジ切削抵抗として次の式が得られます。

\(G=Kf\theta^{1.41}U^{-0.319}EXP(-3.42W)\)

ここで、Kは定数、fはストーンの荷重、Uはエッジとぺブルの相対速度です。この式の意味や応用の詳細に興味のある方は下の論文⁽⁸⁾⁽⁹⁾をご覧ください。

ストーンが氷を削るメカニズムのまとめ

これまで述べたことをまとめると、次のようになります。すなわち、

• １）カーリング・ストーンの底面はドーナツ状のランニング・バンドで特徴づけられます。
• ２）ランニング・バンドの両端はエッジですが、エッジは高さが様々なぺブルに出会うと力学的に作用し、変形や切削によって氷くずを生成します。
• ３）このとき発生するエッジ切削抵抗は、エッジ角が増えると増加し、ストーンの速度あるいは回転速度が増えると減少します。
• ４）エッジ切削抵抗はストーン重心に作用しストーンの運動に影響を与えます。

カーリング場で使われているストーンを調べてみますと、外側エッジ角と内側エッジ角は一緒ではなく、後者が前者より少し大きいことが分かります。エッジ切削モデルでは、このエッジ角の相違に着目し、すべてのぺブルによるエッジ切削抵抗を上式を使って計算しました⁽⁸⁾⁽⁹⁾。その結果によりますと、前面ランニング・バンドの外側エッジに起因する切削抵抗の総和に比べ、後面ランニング・バンドの内側エッジによる切削抵抗の総和がより大きくなります。その結果、ストーン重心には横向きの力が発生し、運動の方向が変わります。この力が、ストーンが曲がる、すなわちカールする原因となると考えられます。

最後に、ストーンが通過すると氷くずが発生することに疑いはありません。今回はその原因がランニング・バンドのエッジによる切削であることを示しました。しかし、生じた氷くずの詳細はほとんど分かっていません。氷くずはぺブルの切削で生じた微小な氷粒子ですが、その粒径や結晶構造などはまだ誰も調べたことがありません。カーリング場で実際に氷くずを採取し顕微鏡観察によって粒径や組成を調べる研究の行われることを期待します。